Demystifying Ghost
My mother loves words. To this day, she insists that I should become a poet. During a road trip when I was little, she introduced me to a game called Ghost, and we would play all the time.
To play Ghost, players take turns choosing letters, creating a growing fragment of a word. The goal is to avoid completing a word while still maintaining the fragment’s property that it begins some word. There are two ways to lose a round: complete a word or fail to produce a word that begins with your fragment when challenged by an opponent. Of course, if the challenge is unsuccessful and you come up with a legitimate word, the challenger loses the round. Only words with more than three letters count. Generally, each player begins with five lives, one for each letter of G-H-O-S-T.
For example, imagine that Ada, Babbage, and Church are playing a friendly game of Ghost. Ada goes first and plays e. Babbage cleverly follows Ada’s e with an n of his own. Play continues: Church plays g, Ada plays i, and Babbage plays n. “Shucks,” Church says. I guess I’ll play e. Ada points and laughs and assigns Church a G for spelling “engine.” Simple enough.
Whenever I played with just my mom, she would start with the letter z. With only two players, it seemed as though there was no way to counter – she always won when she started with z. But luckily, instead of training to become a poet, I learned a little Python; now I’m the dominant Ghost player in the household.
Attention: If you plan to play Ghost with your friends, you should probably stop reading now so you don’t have a tiresome advantage.
When I initially solved Ghost to defeat my mother, I only looked into the two-player case. It turns out that Randall Munroe has, in his infinite wisdom, already solved Ghost for two players. In an effort not to be entirely redundant in this post, I’m sharing a solution here for n players. When Randall and I end up playing with a mysterious third party, he won’t know what hit him.
Enough talk. Let’s solve Ghost.
Pruning a Dictionary
First, we need a dictionary. The most reasonable one I could find is the american-english dictionary that ships with some versions of Ubuntu. (Find it at: https://packages.debian.org/wheezy/wamerican). I’m pretty sure this is the same dictionary Randall used.
You can use any dictionary you want, of course. I’m on OSX right now, so I also have Webster’s Second International built in: /usr/share/dict/web2. It has 234,936 words, most of which I don’t know. Some cursory googling also revealed TWL06, which seems to be a version of the American Scrabble dictionary.
# DICTIONARY = "/usr/share/dict/web2"
# DICTIONARY = "/usr/share/dict/TWL06" # scrabble dictionary
DICTIONARY = "/usr/share/dict/american-english" # abridged ubuntu dictionary
Then, we prune this dictionary to contain only words that are lowercase (Proper Nouns Aren’t Allowed) and more than three letters long:
def is_legal_word(word, min_length):
"""
returns True if the string `word` is longer than min_length
and consists entirely of lowercase letters.
"""
return len(word) >= min_length and word.islower()
def gen_word_list(dictionary, min_length):
"""
returns a list of legal words parsed from a file where
each word is lowercase and seperated by a newline
character.
"""
with open(dictionary, 'r') as w:
words = [line.strip() for line in w if is_legal_word(line.strip(), min_length)]
return words
words = gen_word_list(DICTIONARY, 4)
len(words)
>>> 81995
Lists in Python are great, but they’re not the optimal structure for storing words (and – more importantly – prefixes of words) in this case. Enter the trie (from retrieval). A trie is an ordered tree in which every descendant of a node shares the same prefix. A picture would probably be useful; in the diagram below, each complete word is labeled with an arbitrary numeric key. From Wikimedia commons:

Tries are pretty memory efficient too – as you can see in the figure above, we’re storing 8 words using 11 nodes. Finding if a specific word is in a trie is trivially \(O(l)\) where \(l\) is the length of the word, because all you need to do is spell the word to find it. In an unsorted list, such an operation is \(O(n)\), and it’s \(O(log(n))\) using binary search on a sorted list, where \(n\) is the size of the corpus. Finding common prefixes and similar operations is equivalently easy. We won’t implement a trie or get into the nitty-gritty details – that might be a topic for another day. Luckily, there are already a few implementations of Python tries available. This solution uses datrie.
The first thing to do is make the trie from the corpus we just loaded into memory:
import datrie
import string
def make_trie_from_word_list(word_list):
"""
given a list of lowercase words, constructs a trie
with `None` as each value.
"""
trie = datrie.Trie(string.ascii_lowercase)
for word in word_list:
trie[word] = None
return trie
orig_trie = make_trie_from_word_list(words)
Notice that we’re never going to use a word that has a prefix that is another word. We’ll never get to “rainbow” because somebody will have already lost on “rain.” Let’s prune the trie to contain only words that don’t have legal words as prefixes:
# We'll actually create a whole new trie, because deleting from
# a trie is unpleasant.
def prune_trie(trie):
"""
Given a lowercase datrie.Trie, returns a new trie in which no word
has any prefixes that are also legal words.
"""
prefixless = [word for word in trie.keys() if len(trie.prefixes(word)) == 1]
return make_trie_from_word_list(prefixless)
trie = prune_trie(orig_trie)
len(trie)
>>> 19631
Now we’re in prime Ghost-solving territory.
Solving Ghost
To solve Ghost means to find out which players can lose from every possible game state, assuming all players play perfectly.
We’ll store this solution in another trie, where the keys are every substring in the original trie and the values are sets with the possible losers from that node.
The Algorithm
We could solve this with some clever recursion, but it’s easier to take advantage of the structure of the trie. To determine the losers in every possible game state, we perform a level-order traversal of the trie and follow these rules at every node:
- If the node is a leaf node, then it completes a word. In that case, the loser is
get_turn(word_length, num_players)where word_length is equal to the depth of the trie at the leaf node. - If the node is not a leaf node:
- If all of the node’s children include the current player in the set of losers, then the player is indifferent between options because any move is a losing move. In that case, the set of losers at the current node is the union over all of the children’s losers.
- If there is at least one child whose set of losers does not include the current player, then the current player does not lose and is indifferent between all non-losing options. In that case, the set of losers at the current node is the union over all of the sets of children’s losers that do not include the current player.
For an example, consider a trie with the words “aa”, “ab”, “baa”, “bb”, “bcaa”, “bcab”, “caaaa”, and “caab”:
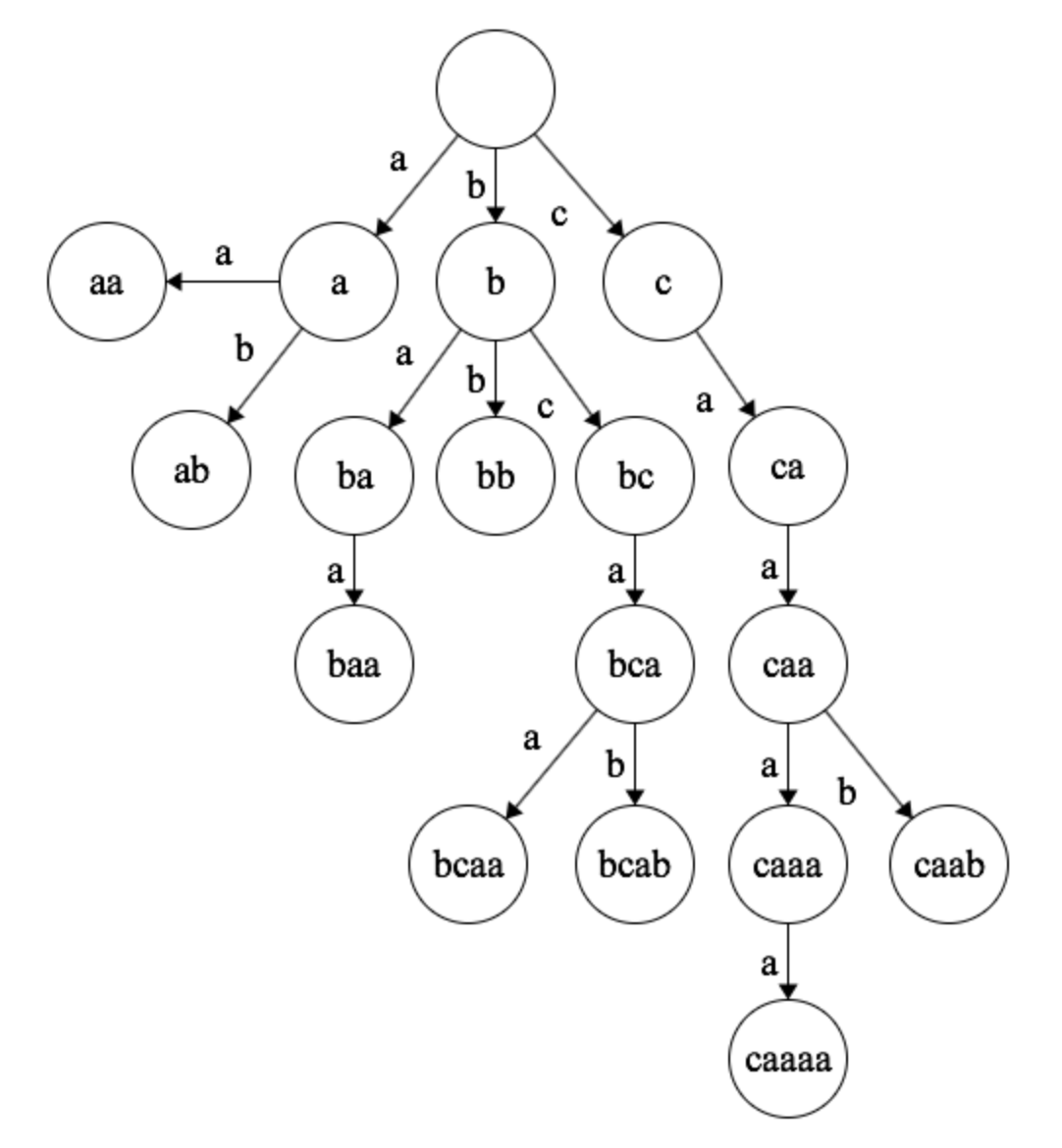
If we follow the algorithm above, then it’s easy to derive the losers at each node:
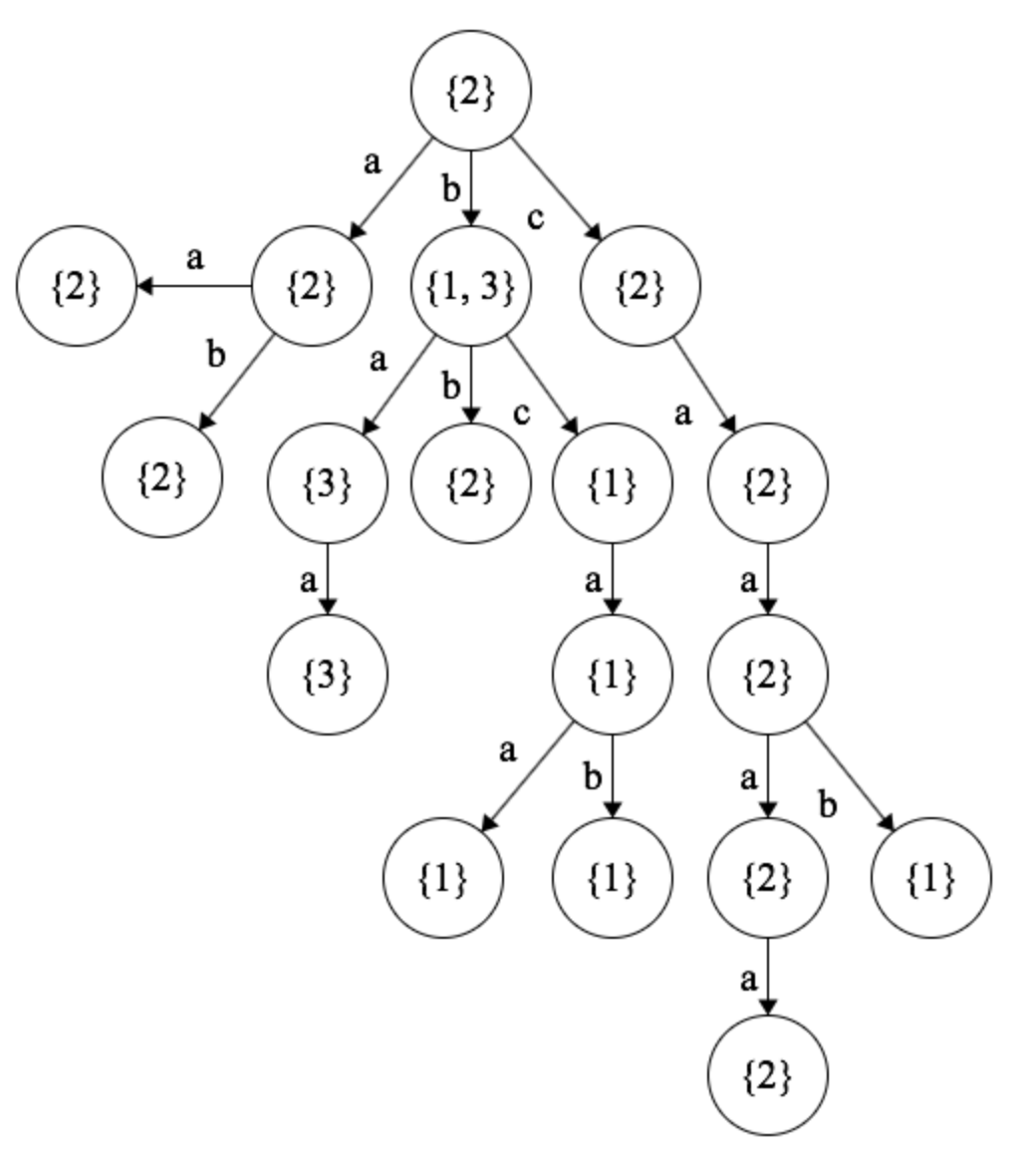
As you can see, player 2 loses. Player 1 will play either ‘a’ or ‘c,’ forcing player 2 into a losing situation. Even though player 1 is not guaranteed to lose with a move of ‘b,’ it counts as a losing node because the other players can coordinate to make player 1 lose.
Finally, it’s time for the actual implementation. Instead of doing a formal level-order traversal, we’re just examining substrings from longest to shortest (ordered arbitrarily within those equivalence classes). This works because once we have solved for all strings of length \(n\), we can solve for all strings of length \(n-1\).
Before we get ahead of ourselves, we need an easy way to find out whose turn it is at any node in the trie:
def get_turn(word_length, num_players):
"""
Returns the id of the player who would finish a word
word_length letters long. Player ids are 1-indexed in
{1... num_players}.
"""
return (word_length - 1) % num_players + 1
print(get_turn(8, 3)) # 1231231**2**
print(get_turn(4, 4)) # 123**4**
print(get_turn(9, 2)) # 12121212**1**
>>> 2
>>> 4
>>> 1
# This function replaces a true level order traveral.
# We need it to specify the keys in our solution trie.
def get_all_substrings(trie):
"""
Parameters:
trie: a datrie.Trie
Returns: a list of all possible substrings of
words in the trie, sorted by length from
longest to shortest.
"""
substrings = set([''])
for word in trie.keys():
substrings.update([word[:p] for p in range(1, len(word))])
substrings = list(substrings)
substrings.sort(key=len, reverse=True)
return substrings
# This is the "meat" of the algorithm that's discussed in the bullets above.
def get_losers(solution, substring, turn):
"""
Parameters:
solution: a datrie.Trie containing the working solution
(must be solved for all substrings longer than substring)
substring: the current position in the trie
turn: the current player
Returns: the set of losers from the node reached by spelling `substring`
"""
# Lists the losers of all of the immediate children
next_losers = [b for a, b in solution.items(substring) if len(a) == len(substring) + 1]
curr_player_loss = set()
other_player_loss = set()
curr_player_loses = True
for loser in next_losers:
if curr_player_loses and turn in loser:
# So far, the current player loses no matter what,
# so the player is indifferent between all losing
# situations.
curr_player_loss |= loser
elif turn not in loser:
# indifferent between all winning situations.
other_player_loss |= loser
curr_player_loses = False
if curr_player_loses:
return curr_player_loss
return other_player_loss
def solve(trie, num_players):
"""
Parameters:
trie: a datrie.Trie, pruned such that there are no
words that have prefixes that are also words
num_players:
the number of players for which to solve
Returns: a 2-tuple (solution, num_players) where `solution`
is a datrie.Trie where every node stores the losing set in its
value. num_players is just along for the ride.
"""
solution_trie = datrie.Trie(string.ascii_lowercase)
substrings = get_all_substrings(trie)
for word in trie.keys():
# base case: complete words
loser = get_turn(len(word), num_players)
solution_trie[word] = set([loser])
for substring in substrings:
# once we have solved for every leaf node, we
# can work our way up the trie.
turn = get_turn(len(substring) + 1, num_players)
solution_trie[substring] = get_losers(solution_trie, substring, turn)
return solution_trie, num_players
Let’s find out who loses from each initial position in a 2-player game.
solution_trie, num_players = solve(trie, 2)
print("\'\'", solution_trie[''])
for c in string.ascii_lowercase:
print(c, solution_trie[c])
'' {2}
a {1}
b {1}
c {1}
d {1}
e {1}
f {1}
g {1}
h {2}
i {1}
j {2}
k {1}
l {1}
m {2}
n {1}
o {1}
p {1}
q {1}
r {2}
s {1}
t {1}
u {1}
v {1}
w {1}
x {1}
y {1}
z {2}
There, Ghost is solved! solution[prefix] gives a set of losers from that prefix. Any self-respecting game theorist would stop now, but I’m neither of those things. It’s no fun to only know who loses with optimal play – it’s a lot better to actually know how to play optimally in any non-doomed situation. This function takes the solution we just computed, along with the current state of the game (some prefix to a word) and returns the winning moves for the current player.
def list_winning_moves(solution, current_state):
"""
Parameters:
solution: the 2-tuple returned from solve
current_state: the incomplete word that has been spelled
so far
Returns: a set of winning moves for the current player. The
empty set if there are no winning moves.
"""
player = get_turn(len(current_state) + 1, solution[1])
winning_moves = set()
if player in solution[0][current_state]:
# player loses, return empty set
return winning_moves
paths = [(a, b) for a, b in solution[0].items(current_state) if len(a) == len(current_state) + 1]
for word, losers in paths:
if player not in losers:
winning_moves.update(word[-1])
return winning_moves
solution = (solution_trie, num_players)
print(list_winning_moves(solution, ''))
print(list_winning_moves(solution, 'h'))
print(list_winning_moves(solution, 'b'))
>>> {'z', 'm', 'j', 'r', 'h'}
>>> set()
>>> {'r', 'l'}
If you arbitrarily choose a letter from the above function, you have an infallible Ghost AI.
Minimal Strategies
Because it would be nearly impossible to memorize optimal moves from every game state, the last task is to find a minimal list of winning words. Some dictionaries have many such lists – this function finds an arbitrary one. First, let’s just find the list of all “winning words,” or those that can be reached without going into a losing state (we’ll store these in a trie again):
def list_winning_words(trie, solution, current_state):
"""
Parameters:
trie: The pruned trie initialized from the dictionary
solution: the 2-tuple returned from solve
current_state: the incomplete word that has been spelled
so far
Returns: the set of winning words for the current player. The
empty set if there are no winning moves.
"""
current_player = get_turn(len(current_state) + 1, solution[1])
winning_words = set(trie.keys(current_state))
for word in trie.keys(current_state):
for substr in (word[:p] for p in range(len(current_state), len(word))):
# If the current player can lose on the way to the winning word,
# it is not a "winning word"
if current_player in solution[0][substr]:
winning_words -= set([word])
continue
return make_trie_from_word_list(list(winning_words))
winning_trie = list_winning_words(trie, solution, '')
To minimize, we recursively examine the size of the winning set that each possible set of moves would create. This is a slow approach with no pruning, but the winning sets at this point are relatively small so it’s not too much of a concern.
def minimize_strategy(winning_trie, solution, current_state):
"""
Parameters:
winning_trie: a trie initialized from the output of list_winning_words
with the same current_state
solution: the 2-tuple returned from solve
current_state: the incomplete word that has been spelled
so far
Returns: the minimal set of winning words for the current player, assuming.
all players play perfectly. The empty set if there are no winning moves.
"""
if current_state in winning_trie:
return set([current_state])
possible_moves = list_winning_moves(solution, current_state)
num_players = solution[1]
best_move = None
for move in possible_moves:
this_move = set()
state = current_state + move
for word in winning_trie.keys(state):
this_move.update(minimize_strategy(winning_trie, solution, word[:len(current_state) + num_players]))
if not best_move or len(best_move) > len(this_move):
best_move = this_move
return best_move
minimize_strategy(winning_trie, solution, '')
>>> {'jail', 'jejune', 'jilt', 'jowl', 'juvenile'}
We can use this function to find a memorizable (or at least minimal) set of winning words from every starting state.
import itertools
def get_minimal_strategies(dictionary, num_players, min_length):
words = gen_word_list(dictionary, min_length)
trie = prune_trie(make_trie_from_word_list(words))
solution = solve(trie, num_players)
for i in range(1, num_players + 1):
print()
print("Player " + str(i) + "'s minimal strategy:")
for prefix in itertools.permutations(string.ascii_lowercase, i - 1):
prefix = ''.join(prefix)
if trie.keys(prefix):
winning_words = list_winning_words(trie, solution, prefix)
s = minimize_strategy(winning_words, solution, prefix)
if not s:
s = "No winning moves."
print(prefix, ": ", s)
get_minimal_strategies(DICTIONARY, 2, 4)
Player 1's minimal strategy:
: {'juvenile', 'jail', 'jilt', 'jowl', 'jejune'}
Player 2's minimal strategy:
a : {'aorta'}
b : {'blimp', 'blemish', 'bloat', 'black', 'blubber'}
c : {'crack', 'crepe', 'crick', 'crozier', 'crypt', 'crept', 'crucial'}
d : {'djinn'}
e : {'ejaculate', 'ejaculation', 'eject'}
f : {'fjord'}
g : {'gherkin', 'ghastliness', 'ghastly', 'ghoul'}
h : No winning moves.
i : {'iffiest'}
j : No winning moves.
k : {'khaki'}
l : {'llama'}
m : No winning moves.
n : {'nymph', 'nylon'}
o : {'ozone'}
p : {'pneumatic'}
q : {'quoit', 'quack', 'quest', 'quibble', 'quibbling'}
r : No winning moves.
s : {'squeeze', 'squelch', 'squeamish', 'squeezing'}
t : {'trochee', 'truffle', 'tryst', 'traffic', 'triumvirate', 'trefoil'}
u : {'uvula'}
v : {'vulva'}
w : {'wrath', 'wrought', 'wrist', 'wrung', 'wryly', 'wreck'}
x : {'xylem'}
y : {'yttrium'}
z : No winning moves.
3+ Players
Below is the minimal strategy for three players. It’s a little unwieldy to memorize, though.
The minimal strategy for 3+ players isn’t particularly useful in a real game, however, because it assumes that all players play perfectly. It’s possible that one of the other 2+ players won’t play in his/her/its own best interest, so the final word could end up being outside any winning strategy.
Interestingly, it’s possible for all 3+ players to be in a losing situation in the same context. Since no player knows what the others will do if indifferent between options, some prefix could be equally “dangerous” for all players.
get_minimal_strategies(DICTIONARY, 3, 4)
Player 1's minimal strategy:
: {'quorum', 'quixotic', 'quest', 'quatrain'}
Player 2's minimal strategy:
a : {'ajar'}
b : {'byes', 'bypass', 'byplay', 'bystander', 'byelaw', 'byproduct', 'byte', 'bygone', 'bypast'}
c : {'czar'}
d : No winning moves.
e : {'eons'}
f : No winning moves.
g : {'gaff', 'gaps', 'gavotte', 'gage', 'gander', 'gantlet', 'gawk', 'gaping', 'gather', 'gave', 'gape', 'gating', 'gang', 'gags', 'gagged', 'gate', 'gannet', 'gaging'}
h : No winning moves.
i : {'iamb'}
j : No winning moves.
k : {'krypton', 'kronor'}
l : No winning moves.
m : {'myna', 'myopia', 'myth', 'myself', 'myopic', 'mysteries', 'mystery'}
n : No winning moves.
o : {'oyster'}
p : {'pneumonia', 'pneumatic'}
q : No winning moves.
r : No winning moves.
s : {'svelte'}
t : {'tzar'}
u : {'ubiquitous'}
v : No winning moves.
w : {'wuss'}
x : No winning moves.
y : {'yttrium'}
z : {'zygote'}
Player 3's minimal strategy:
ab : {'abhor'}
ac : {'acme'}
ad : {'adze'}
ae : {'aegis'}
af : {'afar'}
ag : {'ague'}
ah : {'ahoy'}
ai : {'aisle'}
aj : {'ajar'}
ak : No winning moves.
al : {'alum'}
am : {'amnesia', 'amniocenteses'}
an : {'anus'}
ao : {'aorta'}
ap : {'apse'}
aq : {'aquiline', 'aquiculture', 'aqueous', 'aqueduct', 'aquifer', 'aqua'}
ar : {'arks'}
as : {'asocial'}
at : {'atelier'}
au : {'auxiliaries'}
av : {'avow', 'avoirdupois', 'avocado', 'avoid'}
aw : {'awry'}
ax : {'axon'}
ay : {'ayes'}
az : {'azure'}
ba : {'baffling'}
be : {'bebop'}
bi : {'bizarre'}
bl : {'blow', 'bloc', 'blooper', 'blond', 'bloom', 'blog', 'blossom', 'blood', 'blob', 'bloat', 'blousing', 'blot'}
bo : {'bozo'}
br : {'bras', 'bravado', 'brackish', 'bravo', 'bran', 'brawl', 'brawn', 'bracing', 'brace', 'brag', 'bramble', 'bravura', 'brave', 'brain', 'braising', 'brat', 'braille', 'braving', 'bray', 'braking', 'brad', 'braid', 'bract', 'brake'}
bu : {'buzz'}
by : {'byte'}
ca : {'cayenne'}
ce : {'cephalic'}
ch : {'chlorophyll'}
ci : {'cistern'}
cl : No winning moves.
co : {'cove'}
cr : No winning moves.
cu : {'cuff'}
cy : {'cyanide'}
cz : {'czar'}
da : {'dawdling', 'dawn'}
de : {'demo', 'demur'}
dh : {'dhoti'}
di : {'dibbling'}
dj : {'djinn'}
do : {'doff'}
dr : {'drub', 'drunk', 'drug', 'drudging', 'druid', 'drum'}
du : {'duff'}
dw : {'dwarves', 'dwarf'}
dy : {'dyke'}
ea : {'eave'}
eb : {'ebullience'}
ec : {'ecumenical'}
ed : {'educable'}
ef : No winning moves.
eg : {'egalitarian'}
ei : {'eider'}
ej : {'eject'}
ek : {'eking'}
el : {'elms'}
em : {'emcee'}
en : {'envelop', 'envy', 'envoy'}
eo : {'eons'}
ep : {'epaulet'}
eq : {'equinoctial', 'equestrian', 'equability', 'equilateral', 'equip', 'equivalent', 'equal', 'equidistant', 'equator', 'equities', 'equivalence', 'equinox', 'equanimity'}
er : {'erect'}
es : {'esquire'}
et : {'eternal'}
eu : {'eucalyptus'}
ev : {'ever', 'eves', 'even'}
ew : {'ewer', 'ewes'}
ex : {'exult', 'exude', 'exuberance', 'exuding'}
ey : {'eyrie'}
fa : {'favor'}
fe : {'fever'}
fi : {'five'}
fj : {'fjord'}
fl : {'flea', 'flex', 'fleck', 'fled', 'flee', 'flesh', 'flew'}
fo : {'foyer'}
fr : No winning moves.
fu : {'fuel'}
ga : {'gaff'}
ge : {'gear'}
gh : {'ghoul', 'ghost'}
gi : {'gift'}
gl : {'glee', 'glean', 'glen', 'gleam'}
gn : {'gnus'}
go : {'gown'}
gr : {'gryphon'}
gu : {'guzzling'}
gy : {'gyrating', 'gyration', 'gyro'}
ha : {'haemophilia'}
he : {'heft'}
hi : {'hims'}
ho : {'hock'}
hu : {'huff'}
hy : {'hyena'}
ia : {'iamb'}
ib : {'ibex'}
ic : {'icon'}
id : {'idyl'}
if : {'iffiest', 'iffy'}
ig : {'igloo'}
ik : {'ikon'}
il : {'ilks'}
im : No winning moves.
in : {'inquietude', 'inquest'}
io : {'iota'}
ip : No winning moves.
ir : {'iron'}
is : {'isms'}
it : {'itch'}
iv : {'ivies'}
ja : {'jazz'}
je : {'jewel'}
ji : {'jiujitsu'}
jo : {'jowl'}
ju : {'just'}
ka : {'kazoo'}
ke : {'kestrel'}
kh : {'khaki', 'khan'}
ki : {'kiwi'}
kl : {'klutz'}
kn : {'knavish', 'knave', 'knapsack', 'knack'}
ko : {'koala'}
kr : {'krypton'}
ku : {'kumquat'}
la : {'lallygag'}
le : {'left'}
li : {'lion'}
lo : {'lozenge'}
lu : {'luau'}
ly : {'lymph'}
ma : {'maxed', 'maxes'}
me : {'meow'}
mi : {'miff'}
mn : {'mnemonic'}
mo : {'mozzarella'}
mu : {'muzzling'}
my : {'myth'}
na : {'nays'}
ne : {'need'}
ni : {'nirvana'}
no : {'noxious'}
nu : {'nuzzling'}
ny : {'nymph'}
oa : {'oasis', 'oases'}
ob : {'obit'}
oc : {'ocarina'}
od : {'odes'}
of : {'often'}
og : {'ogre'}
oh : {'ohms'}
oi : {'oink', 'ointment'}
ok : {'okay'}
ol : {'olfactories'}
om : {'ominous', 'omit', 'omission'}
on : {'onion'}
op : {'opossum'}
or : {'orotund'}
os : {'osier'}
ot : {'other'}
ou : {'ours'}
ov : {'ovoid'}
ow : {'owing'}
ox : {'oxbow'}
oy : No winning moves.
oz : {'ozone'}
pa : {'paean'}
pe : {'pejorative'}
ph : {'phrasal', 'phrenology'}
pi : {'pirouetting'}
pl : No winning moves.
pn : No winning moves.
po : {'poxes'}
pr : No winning moves.
ps : {'psalm'}
pt : {'pterodactyl'}
pu : {'puzzling'}
py : {'pyorrhea'}
qu : No winning moves.
ra : {'raja'}
re : {'request', 'requiem'}
rh : {'rhubarb'}
ri : {'riot'}
ro : {'royal'}
ru : {'ruff'}
sa : {'sahib'}
sc : {'scything'}
se : {'sever', 'seven'}
sh : No winning moves.
si : {'sift'}
sk : {'skating', 'skate'}
sl : No winning moves.
sm : {'smear', 'smelt', 'smell'}
sn : {'sneezing', 'sneer', 'sneak'}
so : {'sojourn'}
sp : {'sphinges', 'spheroid'}
sq : No winning moves.
st : No winning moves.
su : {'suturing'}
sv : No winning moves.
sw : {'swum', 'swung'}
sy : No winning moves.
ta : {'tadpole', 'tads'}
te : {'tequila'}
th : {'thalamus', 'that', 'thallium', 'thaw', 'than', 'thalami'}
ti : {'tiff'}
to : {'toque'}
tr : No winning moves.
ts : {'tsar'}
tu : {'tuft'}
tw : No winning moves.
ty : {'tyke'}
tz : {'tzar'}
ub : {'ubiquitous', 'ubiquity'}
ud : {'udder'}
ug : {'ugliness', 'ugliest', 'ugly'}
uk : {'ukulele'}
ul : {'ulcer'}
um : {'umiak'}
un : {'unzip'}
up : {'upend'}
ur : {'uranium'}
us : {'using'}
ut : {'utter'}
uv : {'uvula'}
va : {'vain'}
ve : {'veal'}
vi : {'vixen'}
vo : {'vouch'}
vu : No winning moves.
vy : {'vying'}
wa : {'waffling', 'wafer', 'waft'}
we : {'were'}
wh : {'whys'}
wi : {'wife'}
wo : {'wove'}
wr : {'wrung'}
wu : {'wuss'}
xe : {'xerography', 'xerographic'}
xy : {'xylophonist', 'xylem'}
ya : {'yank'}
ye : {'yews'}
yi : {'yield'}
yo : {'yore'}
yt : {'yttrium'}
yu : {'yule'}
za : No winning moves.
ze : {'zero'}
zi : {'zilch', 'zillion'}
zo : {'zombi'}
zu : {'zucchini'}
zw : {'zwieback'}
zy : No winning moves.
Losers
It is of the utmost importance to decide on a dictionary before partaking in a friendly game of Ghost. Player 2 can win using the Scrabble dictionary, but player 1 always wins with the other two.
| Dictionary | Minimum Word Length | Number of players | Losers | Winning moves for player 1 |
|---|---|---|---|---|
| web2 | 3 | 2 | {2} | {‘a’, ‘h’, ‘l’} |
| web2 | 3 | 3 | {3} | {‘t’, ‘a’, ‘d’, ‘n’} |
| web2 | 3 | 4 | {3, 4} | {‘j’, ‘l’} |
| web2 | 4 | 2 | {2} | {‘a’, ‘h’, ‘l’, ‘e’} |
| web2 | 4 | 3 | {3} | {‘t’, ‘a’, ‘d’} |
| web2 | 4 | 4 | {3, 4} | {‘j’, ‘r’, ‘l’} |
| TWL06 | 3 | 2 | {1} | None |
| TWL06 | 3 | 3 | {3} | {‘m’, ‘n’} |
| TWL06 | 3 | 4 | {3, 4} | {‘h’, ‘q’} |
| TWL06 | 4 | 2 | {2} | {‘m’, ‘n’} |
| TWL06 | 4 | 3 | {1,2,3} | None |
| TWL06 | 4 | 4 | {3, 4} | {‘h’, ‘q’} |
| american-english | 3 | 2 | {2} | {‘j’, ‘m’, ‘h’, ‘z’} |
| american-english | 3 | 3 | {2, 3} | {‘n’, ‘s’, ‘q’, ‘r’, ‘z’, ‘p’} |
| american-english | 3 | 4 | {3, 4} | {‘r’, ‘z’} |
| american-english | 4 | 2 | {2} | {‘j’, ‘m’, ‘h’, ‘r’, ‘z’} |
| american-english | 4 | 3 | {2, 3} | {‘s’, ‘p’, ‘q’} |
| american-english | 4 | 4 | {4} | {‘m’, ‘z’} |
The Moral: if you’re going to play Ghost with your mother, make sure you use the Scrabble dictionary. Then you can win when she plays ‘z.’
Download
To experiment yourself, you can download this post as an iPython notebook. However, I’ve also implemented a more flexible “Ghost” class that you can download here along with a basic test suite here.
As always, any suggestions, corrections, criticisms (constructive or otherwise), and witticisms welcome.